Answers for wk 5:

1) (2012 AMC 10A)
2) (2011 AMC 10A)

Solution (1):

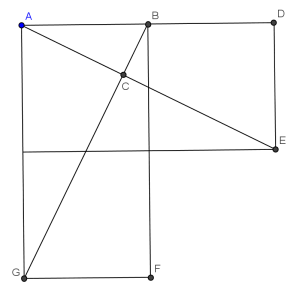
To find the area of triangle ABC, we can find the product of the base and height of the triangle and divide it by two. There are other ways, but seeing that looks like a right angle, one can use this way to derive the area. Obviously, our job now is to prove that . This can be done every easily.

Notice that

Since

(alternate angles, $latex AG // ED $)

Also,

(SAS)

Now that we proved that , we need to find the lengths of AC, BC. I personally would use similar triangles to find the lengths.

Seeing that

(AA)

By Pythagoras',

Solution (2):
Before we attempt this question, one is required to know an important property:

If a,b are both positive integers, then the R.H.S. becomes

, where n=a+b, .

This expression is similar to the expression under the surd in the question. Therefore, we try to express it as a square in the form of in order to remove the square root.

Hence, in the expression

n=a+b=9,

Therefore, we derive the following simultaneous equation:

(2) is equals to:

Solving equations (1) and (3) gives us

(a,b)=(6,3),(3,6). Remember that a,b are positive integers.

When (a,b)=(6,3),

When (a,b)=(3,6),

---