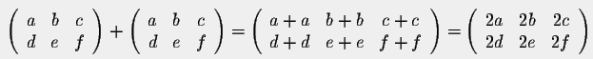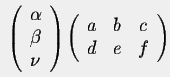The size of the matrix, as a block, is defined by the number of rows and the numver of columns. In this case, the above matrix has 2 rows and 3 columns.
When the number of rows and columns are equal, the matrix can also be known as a square matrix. For example a square of order n, is a (n x n) matrix.
Addition
In order to add to matrices, we have to add the entries one by one.
Also, when adding matrices, make sure they are of the same size.
Multiplication of matrices
Unlike the addition of matrices, multiplying matrices do not require them to be of the same size. However, the general rule says that in order to perform the multiplication AB, where A is a (m x n) matrix and B is a (p x q) matrix, n must be equal to k, which will result in a (m x q) matrix.
Therefore, although these
matrices can be multiplied,
these could not.