Binomial Theorem

Hi everyone, hope our blog posts have not been too messy. The binomial expansion is an extensive expansion that expands the regular expansion. Ok, I'm being lame. Basically, the binomial expansion shows you how $(a+b)^n$ is expanded.

For many of you, you might have noticed that when you expand this sort of equation, the power of a decreases from n to 0 and vice versa for b. Something like this $a^n + a^b^-^1b + ... + ab^n^-^1 + b^n$

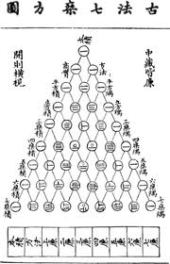
Now, the real question is how to determine the coefficients. And that's where the binomial expansion comes into place. There are 2 main ways. 1) Pascal's / Yang's Triangle 2) Combinatorics 1) Ok so 2 geniuses, Yang and Pascal came up with the triangle independently (surprisingly). Blaise Pascal is a French dude from the 17th Century while Yang Hui is a Chinese dude from the 13th Century. However, it is more commonly known as Pascal's triangle as he published it first.

As you can see from the diagram, the triangles are sort of number pyramids where the next part is the sum of the adjacent parts above. As you can see, the ( n+1)th line gives you the coefficients for $(a+b)^n$ as the 1st line is for the $(a+b)^0$ = 1. So (a+b) = a + b, $(a+b)^5$ = $a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5$ .

2) Combinatoric method. This is especially useful when n > 5 and you're dealing with big badass numbers. You definitely will not be able to afford the time drawing out a nice big pyramid.

Quick Recap: Combinatorics is $\binom{k}{r} = \frac{k!}{r! (k-r)!}$ where a humongous C is used to replace the bracket sometimes.

So anyway, the combinatorics method follows this pattern: $\binom{n}{0} a^ n +\binom{n}{1}a^n^-^1b+ ... + \binom{n}{n-1}ab^n^-^1+\binom{n}{n}b^n$

Here's something to bridge 1) and 2) and help you understand better.

Amazing right?

Here's another interesting part For $n \in N$ , we can derive the formula:

$(x+y)^n=\displaystyle{\sum_{i=0}^n \binom{n}{i}x^{n-i}y^i}$

where $\displaystyle{\binom{n}{i}}$ is the binomial coefficient, satisfying the conditions of $n,i \in N_0, i \leq n$ , and is defined as

$\displaystyle{\binom{n}{i}} = \displaystyle{\frac{n!}{(n-i)!i!}}$ .

Also, an interesting fact to note is that $\displaystyle{\binom{n}{0}+\binom{n}{1}+\binom{n}{2}+...+\binom{n}{n}=2^n}$

This implies that the sum of binomial coefficients of the expression $(x+y)^n$ is $2^n$ . It also comes with an interesting proof:

Let $x,y$ in the binomial formula be 1, which leads us to

$\displaystyle{(1+1)^n=\sum_{i=0}^n\binom{n}{i}1^{n-i}1^i}$

Since the condition for the binomial formula to be true is $n,i \in N_0$ and $i \leq n$ , we can simplify the expression to:

$\displaystyle{2^n=\sum_{i=0}^n\binom{n}{i}}$ , proven.

OK hope that was fun :D etzhkysy