Question
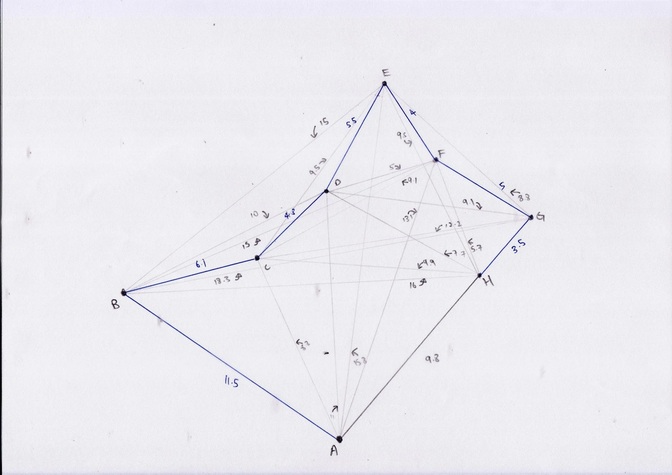
Given that there are 6 people: p, q, r, s, t, and u, and they start from either points A, B, C, D, E, F, G or H, such that no 2 or more people start from the same point, how should these people move such that they end up all at the same point, and:
a) Each person covers the same distance (don't have to be exactly same, just optimize the results to match this condition)
b) The sum of the distance covered is minimized
c) All the points must be visited by at least one person
a) Each person covers the same distance (don't have to be exactly same, just optimize the results to match this condition)
b) The sum of the distance covered is minimized
c) All the points must be visited by at least one person
Solution
(see map: http://sdrv.ms/P4z7Ul)
We see that amongst the lines converging at D, AD is the longest, where AD = 11
If we try and find another destination (end point) whereby the longest line converging there is smaller than AD, we find it impossible:
1) A must be visited, so we look at the lines converging there
2) Find the lines shorter than AD: AC or AH
3) If we make C the destination, CG > AD. If we make H as the destination, BH > AD
So D should be the destination.
I know this doesn't really answer question (a) or (b), but it does help to make sure that we reduce the maximum walking distance for one person.
p.s. we can make person starting at F go to E before going to D, so EF + ED < AD
We see that amongst the lines converging at D, AD is the longest, where AD = 11
If we try and find another destination (end point) whereby the longest line converging there is smaller than AD, we find it impossible:
1) A must be visited, so we look at the lines converging there
2) Find the lines shorter than AD: AC or AH
3) If we make C the destination, CG > AD. If we make H as the destination, BH > AD
So D should be the destination.
I know this doesn't really answer question (a) or (b), but it does help to make sure that we reduce the maximum walking distance for one person.
p.s. we can make person starting at F go to E before going to D, so EF + ED < AD
 RSS Feed
RSS Feed
