Similarity of Triangles

Basically, two triangles are similar if they have a same shape, but different sizes. Technically speaking, the two triangles are similar if their corresponding angles are all equal and all their corresponding sides proportionate.

If two triangles are similar, for example triangle ABC is similar to triangle A'B'C', we denote this as:

$\triangle ABC \sim \triangle A'B'C'$

When we are searching or wanting to prove a pair of similar triangles, we often want to find the ratio of the corresponding sides of the two similar triangles. Now for the corresponding sides of two similar triangles they share an equal ratio, which leads us to this:

$\displaystyle{\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CA}{C'A'}}=k \textup{ ,where } k \textup{ is a constant.}$

So how do we prove that two triangles are indeed similar? Well below are 3 criterion for two triangles to be similar:

Two pairs of corresponding angles are equal. (A.A.)
All corresponding sides are proportionate. (S.S.S.)
Two pairs of corresponding sides are proportionate, and the included corresponding angles are equal. (S.A.S.)

Some of you may ask why isn't condition (1) be (A.A.A.)? Well, if you found two pairs of corresponding angles are equal, the remaining corresponding angles will be also equal, by the fact that the sum of all internal angles of all triangles is 180 degrees. From my experience, you may not use the S.A.S. and S.S.S. criterion in typical problems -- the condition is too obvious and examiners won't want you to solve the problem that quick. Most of the time you have to use the A.A. criteria. I'm not implying that you shouldn't try to use the S.A.S. and S.S.S. criterion in solving problems. I'm just saying that you'll not use those 2 criterion as often as you'll use the A.A. criteria. Another interesting criteria for you to conclude that two triangles are similar is when you see parallel lines.

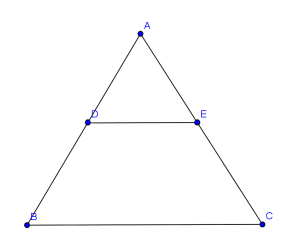
The first diagram shows that triangle ADE is similar to triangle ABC due to the fact that DE // BC.
The second diagram shows that triangle DAE is similar to triangle CBE also due to the fact that DA // BC.
Try figure out why parallel lines make them similar? (Hint: Parallel lines form equal angles when cut by a transversal.)
Also be aware of the fact that for two similar triangles, their corresponding sides, corresponding altitudes, corresponding medians, corresponding angle bisectors, corresponding perimeter are all proportional with the same ratio, k.
And also for two similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding sides. For example, when triangle ABC is similar to triangle A'B'C', we get the condition

$\displaystyle{\frac{S_{\triangle ABC}}{S_{\triangle A'B'C'}}=\left(\frac{AB}{A'B'}\right)^2=\left(\frac{BC}{B'C'}\right)^2=\left(\frac{CA}{C'A'}\right)^2}$

$\textup{where } S_{\triangle ABC}\textup{ denotes the area of triangle ABC.}$

Now some application.. Example 1.
As shown in the diagram below, AB // EF // CD. BEC, DEA and BFD are straight lines. If AB=6, CD=9, what is the length of EF?

Notice there are a lot of similar triangles we can derive from this diagram because of the parallel lines drawn. But what the question has asked for is EF, and we also need to apply what the question has given us, which is the length of AB and CD. In other words, we need to find two similar triangles that has lines AB,CD,EF in it. You should find that there are 2 pair of similar triangles that satisfy the conditions, which is:

$\triangle DEF \sim \triangle DAB $ and $ \triangle BEF \sim \triangle BCD $$

Therefore, we derive the simultaneous equation:

$\displaystyle{\frac{EF}{CD}=\frac{BF}{BC}}$
$\displaystyle{\frac{EF}{AB}=\frac{FC}{BC}}$

$\textup{Adding these 2 equations, we get:}$

$\displaystyle{\frac{EF}{9}+\frac{EF}{6}=\frac{BF+FC}{BC}}$
$\displaystyle{\frac{5EF}{18}=\frac{BC}{BC}=1}$
$$ \therefore EF=3.6 $.$

Example 2
Prove that for any triangle, the angle bisector of any interior angle must cut the opposite side into two segments, such that their ratio is equal to the ratio of the two sides of the angle, correspondingly.
To simplify the problem, look at the diagram below.

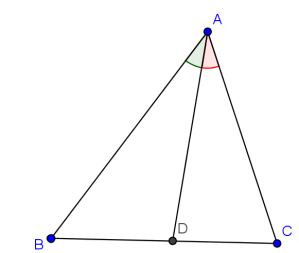
The problem means that in triangle ABC, let AD be the angle bisector of $\angle BAC$ , where AD and BC intersect at D.
What you want to prove is the statement:

$$ \displaystyle{\frac{AB}{AC}=\frac{BD}{CD}} $.$

What you'll probably notice is that there is no similar triangles in this diagram, implying that we need to add auxiliary lines to create them. And the most convenient auxiliary line will be to create a pair of parallel lines.

Therefore, from point C, we introduce CE // AD, intersecting the extension of BA at E. See diagram below for clearer illustration.

Now we found ourselves a pair of similar triangles, triangle BAD and triangle BEC, which implies that

$\displaystyle{\frac{BE}{BA}=\frac{BC}{BD}}$

$\displaystyle{\frac{BE}{BA}-1=\frac{BC}{BD}-1}$

$\displaystyle{\frac{BE-BA}{BA}=\frac{BC-BD}{BD}}$

$\displaystyle{\frac{AE}{BA}=\frac{DC}{BD}}$

$\displaystyle{\frac{AB}{AE}=\frac{BD}{CD}}$

Looks like we're close to our proving statement. So now we need to prove AE=AC, and the proving is done.

And that is easy because of the parallel lines we created.

$$ \angle ECA = \angle DAC = \angle BAD = \angle AEC , \therefore AE=AC $.$

Substituting AE=AC into our last equation, and we're done.

$$ \displaystyle{\frac{AB}{AC}=\frac{BD}{CD}} $.$

In fact, what we had just proved is the angle bisector theorem.

In the last problem we made use one of the proportional properties of segments,

$$ \displaystyle{\frac{a}{b}=\frac{c}{d} \Longrightarrow \frac{a-b}{b}=\frac{c-d}{d}} $,$

where a,b,c,d denote the lengths of line segments.

Other proportional properties of segments include:

$\displaystyle{\frac{a}{b}=\frac{c}{d} \Longrightarrow ad=bc} $$
$\displaystyle{\frac{a}{b}=\frac{c}{d} \Longrightarrow \frac{a+b}{b}=\frac{c+d}{d}} $$
$\displaystyle{\frac{a}{b}=\frac{c}{d} \Longrightarrow \frac{a+b}{a-b}=\frac{c+d}{c-d}} $, if $ a-b\neq 0 $ and $ c-d \neq 0 $$
$\displaystyle{\frac{a}{b}=\frac{c}{d}=\cdots =\frac{m}{n}(bd\cdots n\neq 0) \Longrightarrow \frac{a+c+\cdots +m}{b+d+\cdots +n}=\frac{a}{b}=\frac{c}{d}=\cdots =\frac{m}{n}} $, if $ b+d+\cdots +n\neq 0 $$

where a,b,c,... denote the lengths of line segments.
That's bout all for similarity, hope you learnt something from this post.
Cheers,
etzhkyay =)