Part 1
Hey readers,
Today we are going to learn about the division of polynomials. Back in the basics page, we have already defined polynomials. As this topic is very tricky and tedious and any other scary words you can think of, I’m gonna explain it in parts. (See the title).
OK, first of all, we all would already know what long division is ( I hope…)
Long division is when , where m is the dividend, m is the divisor, q is the quotient and r is the remainder. When r = 0, you can infer that n is divisible by m (and of course q).
This brings us to the division of polynomials. Unlike normal long div, you have to divide terms of different degrees which could prove messy and annoying. To put it briefly, so its a bit like normal division.
and
play the same role as n and m respectively. Hope that clears things up.
Now, how to divide? Lets start with the factor and remainder theorem.
1) For any constant a, a polynomial of degree
can be written as
, q(x) is a polynomial degree of n-1, and r = f(a). When n > 1 ,
2) The Factor Theorem:
A polynomial f(x) has the factor (x-a) if f(a) = 0.
From here, we can see that (x-a) is a divisor as when f(a), (x-a) = 0 i.e. no remainder.
3) Hardcore method / long div method (as seen in video below)
In a nutshell, the long division method is almost the same as your regular long division. Start with the dividend term with the biggest degree and the divisor term of the biggest degree, then go to the 2nd greatest divisor term.
To be continued… Next up, factorization of Symmetric / Cyclic polynomials
etzhkysy
P.S. Here is an awesome video to watch: http://www.youtube.com/watch?v=FXgV9ySNusc&feature=relmfu
Part 2
Hi everyone, happy vesak day!!!!
Symmetric Polynomials
A polynomial with many variables is known as symmetric if it does not change by and permutation of its variables. This means that if x is replaced by y and y is replaced by x, the result is still the same. i.e. x<->y
Eg of symmetric polynomial: so if x and y switch positions, nothing is change.
NOT a symmetric polynomial:
Symmetric expressions containing 2 variables can always be expressed as the basic symmetric expression, i.e. (x+y), xy
For x,y,z, we can factorise em into: x+y+z, xyz, xy + yz +xz
Cyclic Polynomials
A polynomial with many variables is called Cyclic if when the position of its variables change position “simultaneously” resulting in NO change in result. i.e. x -> y -> z -> x
Eg. xy + yz + xz, (x+y)(y+z)(x+z)
Why is this helpful? Because, when you factorise, and discover that one factor is (x+y), you immediately know that (x+z) and (y+z) are factors too because of this cyclic property.
In general, you take one of the variables as a the principal variable, and leave the others as constants for the time being, so that we can get a polynomial of a single variable. After which, we can find factors using the factor theorem and then get to the situation up there ^.^ BTW, you can also use this method for symmetric polynomials too if I’m not wrong.
Random Questions to try:
Factorise:
and
Answers out in another post ![]()
Have a nice day,
etzhkysy
Part 3
Hi everyone,
This post elaborates on div of polynomials 1.
Remember we learnt long div of polynomials? Well, now we’re gonna learn synthetic div briefly, which is really annoying but useful.
In case u forgot, here is the div of polynomials equation:
Synthetic division: When the divisor = x – a, where a is a constant, then
is a polynomial with degree n-1 if the degree of
is n, and the remainder
is a constant.
So, ,
Since,
and by expansion you get,
By comparing the coefficients of ,
we have
and we can come up with an operation table
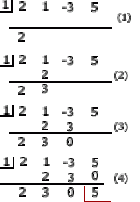 , something like this. I’ll post a better one soon.
, something like this. I’ll post a better one soon.
Here’s a synthetic division calculator I found : http://www.mattdoyle.net/old/synthetic.html
Thkq,
etzhkysy
