Area & Perimeter of Triangles

By looking at the topic, you all might think "Well, I know how to calculate the area and perimeter, that's the basics". Well in this post I won't be covering some primary school stuff. This post aims to bring your knowledge of area and perimeter of triangle to a higher level, so if you think (base)(height)/2 is the only way to calculate the area of triangle, you might want to read this post.

Perimeter of triangles. The most obvious way to obtain it is to add the three sides of the triangle. Enough said.

Area of triangles. Other than the common (base)(height)/2, we have another way of computing the area of a triangle. And this method is related to the perimeter of the triangle.

Ever heard of Heron's formula? If you don't know about it, well pay attention. Heron's formula states that the area S of a triangle whose lengths are a,b,c is

$S=\sqrt{s(s-a)(s-b)(s-c)}$ ,

where $\displaystyle{s=\frac{a+b+c}{2}}$ , also known as the semi-perimeter.

The proof of it is quite.. complicated, so you can ignore it and skip to ** if you feel uncomfortable reading it.

Proof

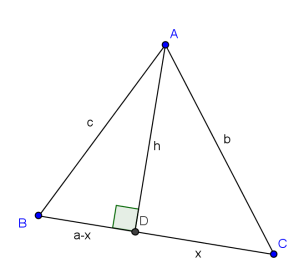
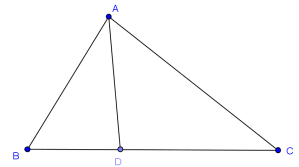
As shown in the diagram above, BC=a, CA=b, AB=c, AD=h, where $AD\perp BC$ at D. Let CD=x, then

$c^2-(a-x)^2=h^2=b^2-x^2$ (By Pythagoras')
$c^2-a^2+2ax-x^2=b^2-x^2$
$\displaystyle{c^2-a^2+2ax=b^2 \Longrightarrow x=\frac{a^2+b^2-c^2}{2a}}$

Therefore,

$\displaystyle{h^2=b^2-\left(\frac{a^2+b^2-c^2}{2a}\right)^2}$ (By Pythagoras')

Simplifying yields

$\displaystyle{=\frac{(2ab)^2-(a^2+b^2-c^2)^2}{4a^2}=\frac{(2ab+a^2+b^2-c^2)(2ab-a^2-b^2+c^2)}{4a^2}}$
$\displaystyle{=\frac{[(a+b)^2-c^2][c^2-(a-b)^2]}{4a^2}=\frac{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}{4a^2}}$
$\displaystyle{=\frac{(2s)(2s-2c)(2s-2b)(2s-2a)}{4a^2}}$ (s denotes the semi-perimeter here.)
$\displaystyle{=\frac{2(s)2(s-c)2(s-b)2(s-a)}{4a^2}=\frac{4s(s-a)(s-b)(s-c)}{a^2}}$

$\displaystyle{\therefore S^2=\left(\frac{ah}{2}\right)^2=\frac{a^2h^2}{4}=s(s-a)(s-b)(s-c)}$ (By substituting $h^2$ into the equation)

$\Longrightarrow S=\sqrt{s(s-a)(s-b)(s-c)}$

Proof Complete.

Another way to calculate the area of a triangle, and is quite commonly used when you reach upper secondary, is using trigonometry. Use the diagram below to aid you in understanding the formula.

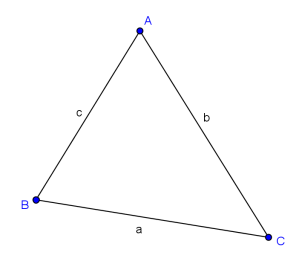
The area S of the triangle ABC is

$\displaystyle{S=\frac{1}{2}ab\sin\angle C=\frac{1}{2}bc\sin\angle A=\frac{1}{2}ca\sin\angle B}$

Another way to interpret the formula is to say that the area of triangle ABC is "Half-ab-sine the included angle". Included angle means the angle in between. At least that's what I heard from other people.

There are also other variations to the formula, but that will require knowledge from trigonometry beforehand, so I won't be covering it in this post.

There is another way to compute the area of a triangle, but this formula only applies for equilateral triangles. Remember, only equilateral triangles. The area of the triangle ABC, with lengths s is equal to

$\displaystyle{S=\frac{\sqrt{3}s^2}{2}}$

The proof is relatively easy, involving only the Pythagoras' theorem.

Comparison of areas of triangles
In solving geometry questions, one can consider using area to solve the problem. Using area to solve a geometry problem often require us to relate the areas of different triangles with the ratio of line segments and hence solving the problem. Below are a few properties that one must know in order to use this technique (I'll provide diagrams to aid you in comprehending the properties):

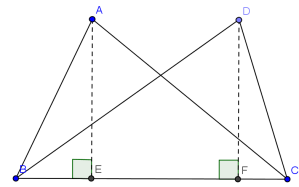
For 2 triangles with equal bases, the ratio of their areas is equal to the ratio of the heights on the bases.

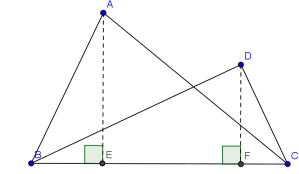
For example, in the above diagram, where [ABC] denote the area of ABC,

$\displaystyle{\frac{[ABC]}{[DBC]}=\frac{AE}{DF}}$

Therefore, the area of 2 triangles are equal if they have equal bases and equal heights on the bases.

For example, in the above diagram, if AE=DF, we have

[ABC]=[DBC].

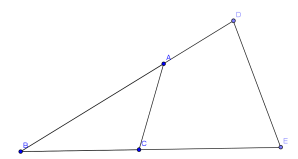
For 2 triangles with equal height, the ratio of their areas is equal to the ratio of their bases.

For example, in the above diagram,

$\displaystyle{\frac{[ABD]}{[ABC]}=\frac{BD}{BC}}$

If 2 triangles have a pair of equal angles, then the ratio of their areas is equal to the ratio of the products of the 2 sides of the equal angles.

For example, in the above diagram,

$\displaystyle{\frac{[ABC]}{[DBE]}=\frac{AB\cdot BC}{DB\cdot BE}}$

For some readers, this property may be a little harder to prove than the 3 properties mentioned earlier. For their benefit, I shall prove this property.

Proof

$\displaystyle{\frac{[ABC]}{[DBE]}=\frac{\frac{1}{2}\cdot AB\cdot BC\cdot\sin\angle ABC}{\frac{1}{2}\cdot DB\cdot BE\cdot\sin\angle DBE}}$

Since $\angle ABC=\angle DBE$ , we have

$\displaystyle{\frac{[ABC]}{[DBE]}=\frac{AB\cdot BC}{DB\cdot BE}}$

Proof complete.

If 2 triangles have a pair of supplementary angles, then the ratio of their areas is equal to the ratio of the products of the two sides of the supplementary angles.

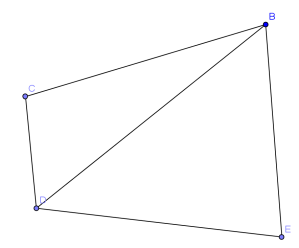
For example, in the above diagram, BCDE is a cyclic quadrilateral. This implies that $\angle BCD+\angle BED=180^{\circ}$ .

$\displaystyle{\Longrightarrow\frac{[BCD]}{[BED]}=\frac{BC\cdot CD}{BE\cdot ED}}$

The proof of this involves some basic trigonometric properties, so if you do not understand the proof, just ignore it and skip to **.

Proof

$\displaystyle{\frac{[BCD]}{[BED]}=\frac{\frac{1}{2}\cdot BC\cdot CD\cdot\sin\angle BCD}{\frac{1}{2}\cdot BE\cdot ED\cdot\sin\angle BED}}$

Since $\sin\alpha =\sin (180^{\circ}-\alpha )$ for all $0^{\circ}\leq\alpha\leq 90^{\circ}$ and $\angle BCD=180^{\circ}-\angle BED$ , we have

$\sin\angle BED=\sin (180^{\circ}-\angle BED)=\sin\angle BCD$

Hence the original equality becomes

$\displaystyle{\frac{[BCD]}{[BED]}=\frac{BC\cdot CD}{BE\cdot ED}}$

Proof Complete.
**

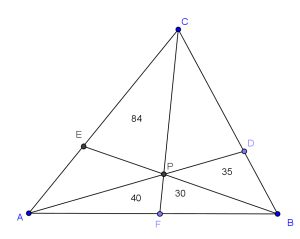
As seen in the diagram below, if ABCD is a convex quadrilateral and their diagonals intersect at O, then we have $\displaystyle{\frac{[CDB]}{[ADB]}=\frac{OC}{OA}}$ and $\displaystyle{\frac{[BCA]}{[CDA]}=\frac{OB}{OD}}$

The proof of this has something to do with the properties of ratios, mentioned in the 'Similarity of Triangles' post. Check it out if you're unfamiliar with those.

Proof

Since

$\displaystyle{\frac{OC}{OA}=\frac{[CDO]}{[DOA]}=\frac{[COB]}{[BOA]}}$

by the property $\displaystyle{\frac{a+b}{c+d}=\frac{a}{c}=\frac{b}{d}}$ , we have

$\displaystyle{\frac{[CDO]+[COB]}{[DOA]+[BOA]}=\frac{OC}{OA}}$

$\displaystyle{\frac{[CDB]}{[ADB]}=\frac{OC}{OA}}$

Similarly, we can also prove that $\displaystyle{\frac{[BCA]}{[CDA]}=\frac{OB}{OD}}$ .

Proof Complete.

Enough of theories, let's proceed to some questions.

Example 1

(AIME/1985) As shown in the diagram below, triangle ABC is divided into six smaller triangles by lines drawn from the vertices through a common interior point P. The areas of four of these triangles are as indicated. Find the area of triangle ABC.

Firstly let [CPD] = x and [EPA] = y.

Notice that we can use area to relate triangles to deduce the ratio of their line segments.

Hence,

$\displaystyle{\frac{[CAP]}{[FAP]}=\frac{CP}{FP}=\frac{[CBP]}{[FBP]}}$

$\displaystyle{\frac{84+y}{40}=\frac{x+35}{30}}\textup{ -----(1)}$

Note that if we want to solve for x,y, we need another equation consisting of x,y. Thus we find another pair of triangles that we can relate:

$\displaystyle{\frac{[CAP]}{[CDP]}=\frac{AP}{DP}=\frac{[BAP]}{[BDP]}}$

$\displaystyle{\frac{84+y}{x}=\frac{70}{35}=2}\textup{ -----(2)}$

From (2), we get

84+y=2x ----- (3)

Hence substituting (3) into (1) gives us

$\displaystyle{\frac{x}{20}=\frac{x+35}{30}}$

Solving for x gives us x=70.

Then, from (3), we plug in x's value and get y=56.

$\therefore [ABC]=84+56+40+30+35+70=315$

Example 2

(SMO(J)/2010) Suppose the three sides of a triangular field are all integers, and its area equals the perimeter. What is the largest possible area of the field?

Actually, other than the first part of the solution, the remaining is all algebra. Nonetheless, the question involves both area and perimeter, so I think it is worth sharing.

The first step, and the most obvious step, is to let the three sides of the triangle be a,b,c respectively. Then we derive the equation

$\sqrt{s(s-a)(s-b)(s-c)}=a+b+c=2s$