So 2 of our group members qualified to participate in SMO(J) Round 2, and the two of us decided to write a post about it, sharing the solutions of the questions. Note that the solutions can be quite hard or complicated for some questions, so don't worry if you can't interpret the solutions. There are a total of 5 questions:
1) Let O be the centre of a parallelogram ABCD and P be any point in the plane. Let M,N be the midpoints of AP,BP respectively and Q be the intersection of MC and ND. Prove that O,P and Q are collinear.
2) Does there exist an integer A such that each of the ten digits 0,1,...,9 appears exactly once as a digit across all of the three numbers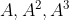
?
3) In triangle ABC, the external bisectors of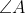
and 
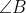meet at the point D. Prove that the circumcentre of triangle ABD and the points C,D lie on the same straight line.
4) Determine the values of the positive integer n for which the following system of equations has a solution in positive integers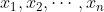
. Find all solutions for each such n.
5) Suppose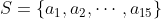
is a set of 15 distinct positive integers chosen from 
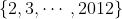such that every two of them are coprime. Prove that S contains a prime number. (Note: Two positive integers m,n are coprime if their only common factor is 1.)
Solutions Q1 (Zhe Hui)
For a clearer picture, refer to the diagram below.
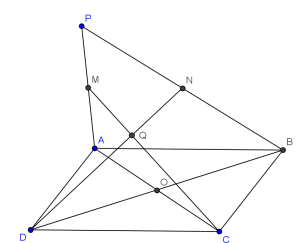
Yeah.. I know the diagram is a bit complicated.. it gets even more complicated later.
Notice there are not 2, but 4 pairs of midpoints.
Yes, I am not kidding. we have
,
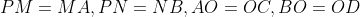by the well-known property that diagonals of parallelograms bisect each other. (If you don't recognize this property look back to your Sec 1 stuff)
This inspires us to join the lines PD, PC to complete the triangles.
Hence, we have the diagram:
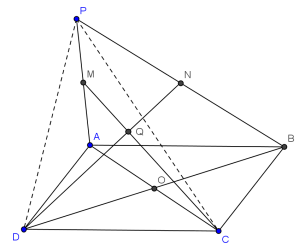
By looking at triangles PAC and PBD, we can see that:
1) The centroid (intersection point of 3 medians -- the 3 medians are concurrent (intersect at the same one point) -- try to prove it?) of triangle PAC is the intersection point of lines OP,MC and let it be named R.
2) The centroid of triangle PBD is the intersection point of lines OP,ND and let it be named S.
By the fact that the centroid must partition the median into two line segments with the ratio 2:1 (Try proving it? It is the theorem on centroid), the centroids of the 2 triangles mentioned earlier must be the same point on line OP, in other words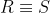
.
Since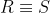, therefore MC,ND,OP are concurrent.
Since the intersection point of lines MC,ND is Q, we get the conclusion that Q must be on the line OP, and thus O,Q,P are collinear (all three points lie on the same straight line).
Q2 (Zhe Hui)
Since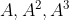 has 10 digits in total, A must be a 2-digit integer.
Hence, we deduce that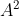
must be a 3-digit integer and 
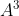must be a 5-digit integer to satisfy the condition.
Since there must be no two same digits across all three numbers, by checking individually, we get:
22 fails automatically
23 fails because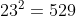
24 fails because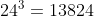
25 fails because the unit digit of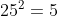
26 fails because the unit digit of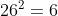
27 fails because
28 fails because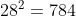
29 fails because the unit digit of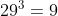
30 fails because the unit digit of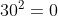
31 fails because the unit digit of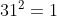
Hence there is no such integer A.
Q3 (Zhe Hui+Ethan)
Again, for a clearer picture, we have the following diagram below for reference:
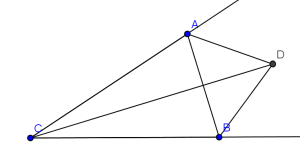
Yes, it is obviously simpler than the diagram before. Just a normal triangle, and 2 angle bisectors of the exterior angles.
Some of you may ask.. what is a circumcentre?
There are actually '5 centers' in a triangle. We will soon write a post about them, and will cover them in details. Here is the brief introduction to the 5 centres:
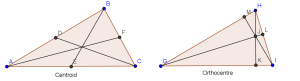
Notice that the question's diagram look extremely alike with the diagram of excentre.
In fact, it is the same diagram, technically. Why? Well here's your answers..
The question states the 2 conditions: the 2 lines bisecting the 2 of the exterior angles meet at a point. Since we know that the excentre is the intersection of 2 exterior angle bisectors and 1 angle bisector, this means that the 3 lines are all concurrent.
If 3 lines are concurrent, they imply that if we have the intersection point of 2 of the lines, the third line must intersect the 2 other lines at their intersection point.
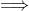CD is the angle bisector of 
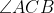and D is the excentre of triangle ABC .
For those that doesn't know, there is an interesting property between an exterior angle bisector and an angle bisector:
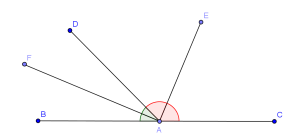
BC is a straight line, AF is the angle bisector of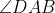
and AE is the exterior angle bisector of 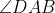. Then, 
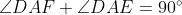. The proof is relatively easy, so I won't be showing that.
Since we have 2 exterior angle bisectors in the question's diagram, we are then inspired to construct angle bisectors. Hence, the diagram becomes:
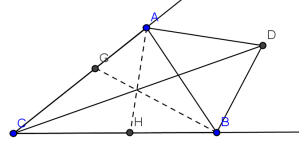
where AH is the angle bisector of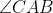
and BG is the angle bisector of 
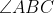. Notice that AH, BG,CD are concurrent, since they are all angle bisectors of triangle ABC.
The intersection point of the three lines is the incentre of triangle ABC
Also, from the property mentioned earlier, we have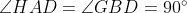
.
We let the incenter of triangle ABC be named I.
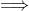The points A,I,B,D are concylic (The 4 points form a cyclic quadrilateral) since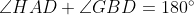 
Till now, the diagram should look like
Since 3 non-collinear points form a unique circle, the circle formed by points A,B,D is the same as the circle formed by points A,I,B,D.
We now use some circle properties (which we will cover in our future posts).
By the property that states any angle subtended by a semicircle arc will be always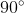
, we deduce that ID is the diameter of the circle formed by points A,I,B,D.
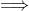The center of the circle formed by points A,I,B,D is on the line ID, and the circumcentre of triangle ABD is the same point as the center of the circle formed by points A,I,B,D, hence we had proven that the circumcentre of triangle ABD is lies on the line CD.
Q4 (Ethan+Zhe Hui)
This question may be impossible to solve if one doesn't have knowledge about the AM-HM or Cauchy's inequality (I haven't found an alternative solution that doesn't make use of these 2 inequalities). So from the AM-GM-HM inequality, we get:
}{n}%20\geq%20\sqrt[n]{a_1a_2...a_n}%20\geq%20\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+...+\frac{1}{a_n}} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Since only AM and HM are useful in this question, after simplifying yields:
Since all n are positive integers,
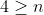
Therefore n=1,2,3,4
We also can make use of Cauchy's inequality to make a range for $latex n $, and it is more straightforward. By Cauchy's, we have:
Since both equality cases happens at n=4, the only solution to n=4 is when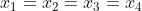
, which is indeed 4.
=(4,4,4,4) "\therefore (x_1,x_2,x_3,x_4)=(4,4,4,4)")
is the only solution for n=1,2,3,4.
Q5 (Ethan+Zhe Hui)
We are trying to disprove the statement that says 'there must be at least 1 prime number in S', so the most logical way is to use contradiction. We assume that there is a set S that has no prime number in its elements.
Since all 15 elements of S must be coprime, they must have different prime factors. If the elements have only 1 prime factor, then the element is prime. Therefore, each element is S must have at least 2 prime factors (not necessarily distinct as it will use up the primes faster). We see that the optimum S is to let all its elements be a square of a prime.
Largest square of a prime: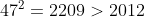
2nd largest: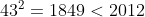
Therefore, the elements in S can only range from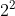
to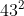 
.
However, there are only 14 primes from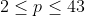
, where p is a prime number.
Therefore, our assumption does not stand, and there must be at least 1 prime in the set S.
1) Let O be the centre of a parallelogram ABCD and P be any point in the plane. Let M,N be the midpoints of AP,BP respectively and Q be the intersection of MC and ND. Prove that O,P and Q are collinear.
2) Does there exist an integer A such that each of the ten digits 0,1,...,9 appears exactly once as a digit across all of the three numbers
3) In triangle ABC, the external bisectors of
4) Determine the values of the positive integer n for which the following system of equations has a solution in positive integers
5) Suppose
Solutions Q1 (Zhe Hui)
For a clearer picture, refer to the diagram below.
Yeah.. I know the diagram is a bit complicated.. it gets even more complicated later.
Notice there are not 2, but 4 pairs of midpoints.
Yes, I am not kidding. we have
by the well-known property that diagonals of parallelograms bisect each other. (If you don't recognize this property look back to your Sec 1 stuff)
This inspires us to join the lines PD, PC to complete the triangles.
Hence, we have the diagram:
By looking at triangles PAC and PBD, we can see that:
1) The centroid (intersection point of 3 medians -- the 3 medians are concurrent (intersect at the same one point) -- try to prove it?) of triangle PAC is the intersection point of lines OP,MC and let it be named R.
2) The centroid of triangle PBD is the intersection point of lines OP,ND and let it be named S.
By the fact that the centroid must partition the median into two line segments with the ratio 2:1 (Try proving it? It is the theorem on centroid), the centroids of the 2 triangles mentioned earlier must be the same point on line OP, in other words
Since
Since the intersection point of lines MC,ND is Q, we get the conclusion that Q must be on the line OP, and thus O,Q,P are collinear (all three points lie on the same straight line).
Q2 (Zhe Hui)
Since
Hence, we deduce that
Since there must be no two same digits across all three numbers, by checking individually, we get:
22 fails automatically
23 fails because
24 fails because
25 fails because the unit digit of
26 fails because the unit digit of
27 fails because
28 fails because
29 fails because the unit digit of
30 fails because the unit digit of
31 fails because the unit digit of
Hence there is no such integer A.
Q3 (Zhe Hui+Ethan)
Again, for a clearer picture, we have the following diagram below for reference:
Yes, it is obviously simpler than the diagram before. Just a normal triangle, and 2 angle bisectors of the exterior angles.
Some of you may ask.. what is a circumcentre?
There are actually '5 centers' in a triangle. We will soon write a post about them, and will cover them in details. Here is the brief introduction to the 5 centres:
- Circumcentre - Intersection of the 3 perpendicular bisectors
- Incentre - Intersection of the 3 angle bisectors
- Centroid (We covered them in Q1) - Intersection of the 3 medians
- Orthocentre - Intersection of the 3 altitudes
- Excentre - Intersection of an angle bisector and 2 exterior angle bisectors on the opposite side.
Yes, they 3 cevians are all concurrent. (Prove it? Hint: Ceva's Theorem)
The diagrams below are to demonstrate each of the 'centres'. (Click on them for a magnified picture)
Notice that the question's diagram look extremely alike with the diagram of excentre.
In fact, it is the same diagram, technically. Why? Well here's your answers..
The question states the 2 conditions: the 2 lines bisecting the 2 of the exterior angles meet at a point. Since we know that the excentre is the intersection of 2 exterior angle bisectors and 1 angle bisector, this means that the 3 lines are all concurrent.
If 3 lines are concurrent, they imply that if we have the intersection point of 2 of the lines, the third line must intersect the 2 other lines at their intersection point.
For those that doesn't know, there is an interesting property between an exterior angle bisector and an angle bisector:
BC is a straight line, AF is the angle bisector of
Since we have 2 exterior angle bisectors in the question's diagram, we are then inspired to construct angle bisectors. Hence, the diagram becomes:
where AH is the angle bisector of
Also, from the property mentioned earlier, we have
We let the incenter of triangle ABC be named I.
Till now, the diagram should look like
Since 3 non-collinear points form a unique circle, the circle formed by points A,B,D is the same as the circle formed by points A,I,B,D.
We now use some circle properties (which we will cover in our future posts).
By the property that states any angle subtended by a semicircle arc will be always
Q4 (Ethan+Zhe Hui)
This question may be impossible to solve if one doesn't have knowledge about the AM-HM or Cauchy's inequality (I haven't found an alternative solution that doesn't make use of these 2 inequalities). So from the AM-GM-HM inequality, we get:
Since only AM and HM are useful in this question, after simplifying yields:
Since all n are positive integers,
Therefore n=1,2,3,4
We also can make use of Cauchy's inequality to make a range for $latex n $, and it is more straightforward. By Cauchy's, we have:
, directly.
Therefore n=1,2,3,4 $.
Now we need to solve the x's. Note that x can only be positive integers.
It is obvious that x has no solution if n=1,2.
For n=3, by substitution and trial and error, we arrive at the conclusion that there are no solution for .
Since both equality cases happens at n=4, the only solution to n=4 is when
Q5 (Ethan+Zhe Hui)
We are trying to disprove the statement that says 'there must be at least 1 prime number in S', so the most logical way is to use contradiction. We assume that there is a set S that has no prime number in its elements.
Since all 15 elements of S must be coprime, they must have different prime factors. If the elements have only 1 prime factor, then the element is prime. Therefore, each element is S must have at least 2 prime factors (not necessarily distinct as it will use up the primes faster). We see that the optimum S is to let all its elements be a square of a prime.
Largest square of a prime:
2nd largest:
Therefore, the elements in S can only range from
However, there are only 14 primes from
Therefore, our assumption does not stand, and there must be at least 1 prime in the set S.
