The 5 Centers of a Triangle
There are actually '5 centers' in a triangle. Here is the brief introduction to the 5 centres:


- Circumcentre - Intersection of the 3 perpendicular bisectors
- Incentre - Intersection of the 3 angle bisectors
- Centroid (We covered them in Q1) - Intersection of the 3 medians
- Orthocentre - Intersection of the 3 altitudes
- Excentre - Intersection of an angle bisector and 2 exterior angle bisectors on the opposite side.
Yes, they 3 cevians are all concurrent. (Prove it? Hint: Ceva's Theorem)
The diagrams below are to demonstrate each of the 'centres'. (Click on the pictures for a magnified view)


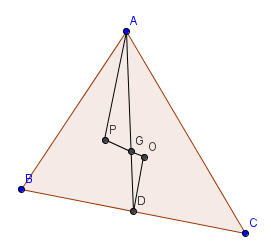
Example 1 - The Euler's Line
Prove that the orthocenter H, centroid G, and circumcenter O of an arbitrary triangle (not equilateral) lie on a line (Euler’s line) and satisfy
Prove that the orthocenter H, centroid G, and circumcenter O of an arbitrary triangle (not equilateral) lie on a line (Euler’s line) and satisfy
The overhead arrow is a symbol that denotes the direction of a line. In this case, since there is an equal sign, we can deduce that both line HG and GO are in the same direction.
The question specified the triangle as not equilateral. This is because the centroid, orthocenter, circumcenter of an equilateral triangle is in fact, the same point.
The phrasing of the question implies that the orthocenter, centroid and circumcenter of any arbitrary triangle (not equilateral) are collinear.
Hence, by joining line OG and define H on line OG, we can prove the theorem.
Therefore, extend OG to a point P, such that
The question specified the triangle as not equilateral. This is because the centroid, orthocenter, circumcenter of an equilateral triangle is in fact, the same point.
The phrasing of the question implies that the orthocenter, centroid and circumcenter of any arbitrary triangle (not equilateral) are collinear.
Hence, by joining line OG and define H on line OG, we can prove the theorem.
Therefore, extend OG to a point P, such that
We shall now prove that point P is the orthocenter H.
Firstly, we construct the median AD, where D is the midpoint of BC.
Firstly, we construct the median AD, where D is the midpoint of BC.
Then, we notice that triangles OGD and PGA are in fact, similar, since
Therefore,
Since OD is the perpendicular bisector of BC,
So AP is the height of triangle ABC. Repeating the same arguments for the other medians proves that P lies on the three heights and therefore must be the orthocenter H. Also, the ratio we determined beforehand becomes 2OG=GH, which ultimately proves the theorem.