Hi readers,

What is trigonometry?

Well, trigo (for short) is actually using functions (trigo functions udunsay) to represent the different ratios of the sides of a triangle. Here are the basic functions and they are most easily understood in a right angle triangle.

Look at the picture. The words like "adjacent" and "opposite" for the respective sides is actually relative to angle A.

So, using angle A, we have

sin A = a/c = opp/hyp ---- sine function           cos A = b/c = adj/hyp----- cosine function

tan A = a/b = opp/adj ---- tangent function      cot A = b/a = adj/opp ------cotangent function

sec A = c/b = hpy/adj ----- secant function     cosec A or csc A = c/a = hyp/opp ------- cosecant function

Opposite means opposite the said angle and adjacent is loosely said, the side "touching the angle"

(of the 2 sides, it is the one that is not the hypotenuse)

Adjacent and opposite are relative to the said angle like in this case, it is A. However, the hypotenuse is fixed and is the "diagonal side". 

TRIGO FUNCTIONS FOR ANY ANGLE

If you look closely, the angle we are studying looks like some funny circle / oval with a line.

It is called, tita (no sick thoughts please)

Basically,

sin (tita) = y/r,   cosine (tita) = x/r

tan (tita) = y/x,  cotangent (tita) = x/y

sec (tita) = r/x,   cosecant (tita) = r/y

Here, the idea is that we use the triangles' sides and plot them in a graph. It dosent have to be a right triangle although the figure seems to suggest so. If the triangle was not a right triangle, you can still split it up into a few right angled triangles.

 

Sine wave:

This is the range of the sine function -> (-1,1), as visible from the graph.

Sine is not a strictly increasing or decreasing function.

Cosine wave:

The range of values for cosine is also (-1,1)

So, the graph show y = sin x. And y = cos x.  The different points of y show the different results of the respective functions on x.

 

Cotangent grpah:

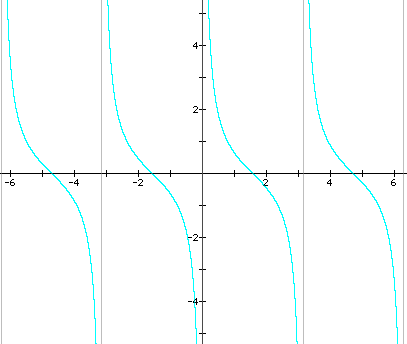  Tangent graph:

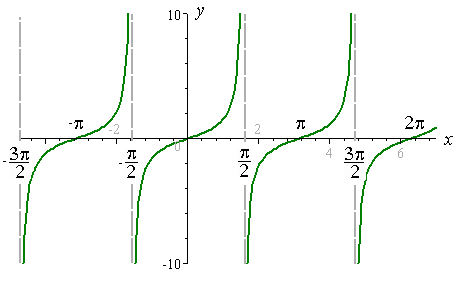
As you can see, the tangent graph and cotangent graph are opposite functions which is true.

Remember  this from just now? tan (tita) = y/x,  cotangent (tita) = x/y

Oh, and yes, why is there the pi there?

Well, pi is actually equal to 90degrees and this is explained by radians which we'll post later on.

Here is some more info:

tangent and cotangent rage: -pi, +pi

 

This graph shows whether the function is positive or negative, based on the quadrant the triangle is drawn in.

It is also known as ASTC - all positive, sine positive, tangent positive, cosine positive

a more complicated version:

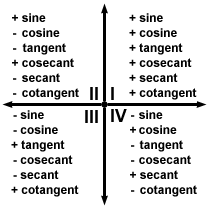
THe graph of all the functions:

  Thanks!
Stay Tuned :)

ethzkyay